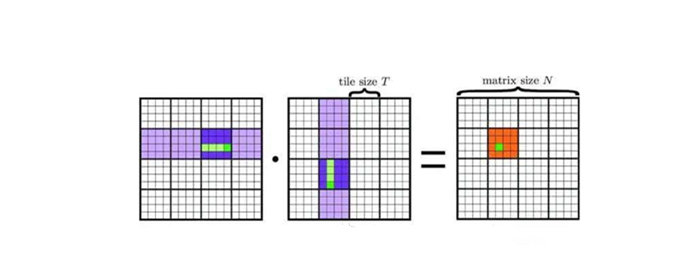
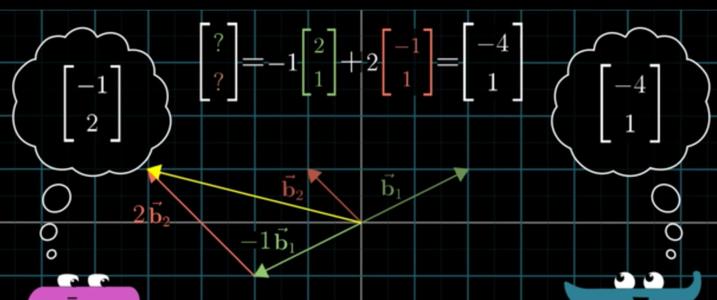
两个矩阵相乘怎么算?
时间:2022-12-25 11:52 来源:未知 作者:今非昔比MSN 点击:载入中...次
| 01 矩阵相乘需要前面矩阵的行数与后面矩阵的列数相同方可相乘。第一步,先将前面矩阵的每一行分别与后面矩阵的列相乘,作为结果矩阵的行列;第二步算出结果即可。
矩阵相乘最重要的方法是一般矩阵乘积。它只有在第一个矩阵的列数(column)和第二个矩阵的行数(row)相同时才有意义 。一般单指矩阵乘积时,指的便是一般矩阵乘积。一个m×n的矩阵就是m×n个数排成m行n列的一个数阵。由于它把许多数据紧凑的集中到了一起,所以有时候可以简便地表示一些复杂的模型。矩阵相乘需要前面矩阵的行数与后面矩阵的列数相同方可相乘。第一步,先将前面矩阵的每一行分别与后面矩阵的列相乘,作为结果矩阵的行列;第二步算出结果即可。
注意事项: 1、当矩阵A的列数等于矩阵B的行数时,A与B可以相乘。 2、矩阵C的行数等于矩阵A的行数,C的列数等于B的列数。 3、乘积C的第m行第n列的元素等于矩阵A的第m行的元素与矩阵B的第n列对应元素乘积之和。
乘法结合律: (AB)C=A(BC) 乘法左分配律:(A+B)C=AC+BC 乘法右分配律:C(A+B)=CA+CB 对数乘的结合性k(AB)=(kA)B=A(kB) 矩阵乘法在以下两种情况下满足交换律。 AA*=A*A,A和伴随矩阵相乘满足交换律。 AE=EA,A和单位矩阵或数量矩阵满足交换律。
还有其他一些特殊的“乘积”形式被定义在矩阵上,值得注意的是,当提及“矩阵相乘”或者“矩阵乘法”的时候,并不是指代这些特殊的乘积形式,而是定义中所描述的矩阵乘法。在描述这些特殊乘积时,使用这些运算的专用名称和符号来避免表述歧义。 (责任编辑:ku987小孩) |